Deformable Models for the Segmentation of Medical Images

contact:
Gunnar Seemann, Olaf Dössel
project group: Image Processing

Project Description

Motivation

In the last years medical images and methods of digital image processing were increasingly applied to aid the diagnosis of various pathologies. Imaging systems like

ultrasonic tomography (US)
computed tomography (CT)
magnet resonance tomography (MRT)

and the methodes of digital image processing are continously improved to obtain images with higher quality.

A main step of the image processing is the segmentation, which delivers homogenous regions. The segmentation is aggravated by artefacts in the images, eg unavoidable motion artefacts by respiration and blood flow.

An appropriate method to segment medical images with artefacts are deformable contours in combination with image filters. The application of deformable contours takes advantage of a-priori knowledge concerning the position and form of an anatomical structure.

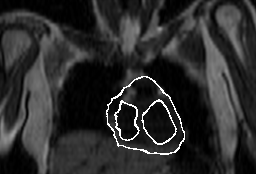
Frontal MRT image of a thorax

Basics

The mostly used representant of deformable models is the so called snake, which uses a-priori knowledge by definition and parametrisation of an energy term as well as by the placement of the initial model in the images. Hereby, the images are two-dimensional and the segmentation process is iterative.

A given deformable model is modified taking the energy term into account until the energy is minimal, eg by excplicit Euler-forward-integration. The energy term consists of internal deformation energies

tension
rigidity etc.

and external energies

image energy, calculated by gradient of image extraction
attractors etc.

In the last time, different methods are published, which extend the deformable model to three dimensions. This task was not possible with previous generations of computers, because of the enormous effort of memory and compute power.

Here presented is a 3D variant of the deformable models, a so called balloon [Werner98]. The foundation of the contour is a triangle mesh. The positions of the nodes are moved aiming at the minimization of the user defined energy term.

A visualization of the segmentation process is an important aid to understand the behaviour of the model and to control it efficiently. Therefore, different methods are created to visualize the segmentation process in 2 and 3 dimensions.

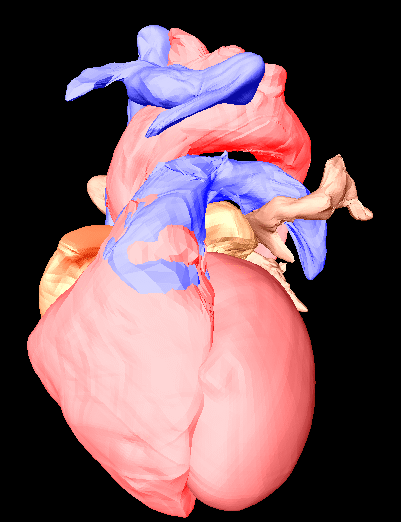
Segmentation of a heart in MRT images

Segmentation of liver and skin in MRT images

Segmentation of body surface (Animation in Quicktime format 3.5 MB)

Segmentation of 4D Data

A method is presented, which allows the efficient segmentation of 4D MRT data and the creation of a dynamic heart model [Busch98].

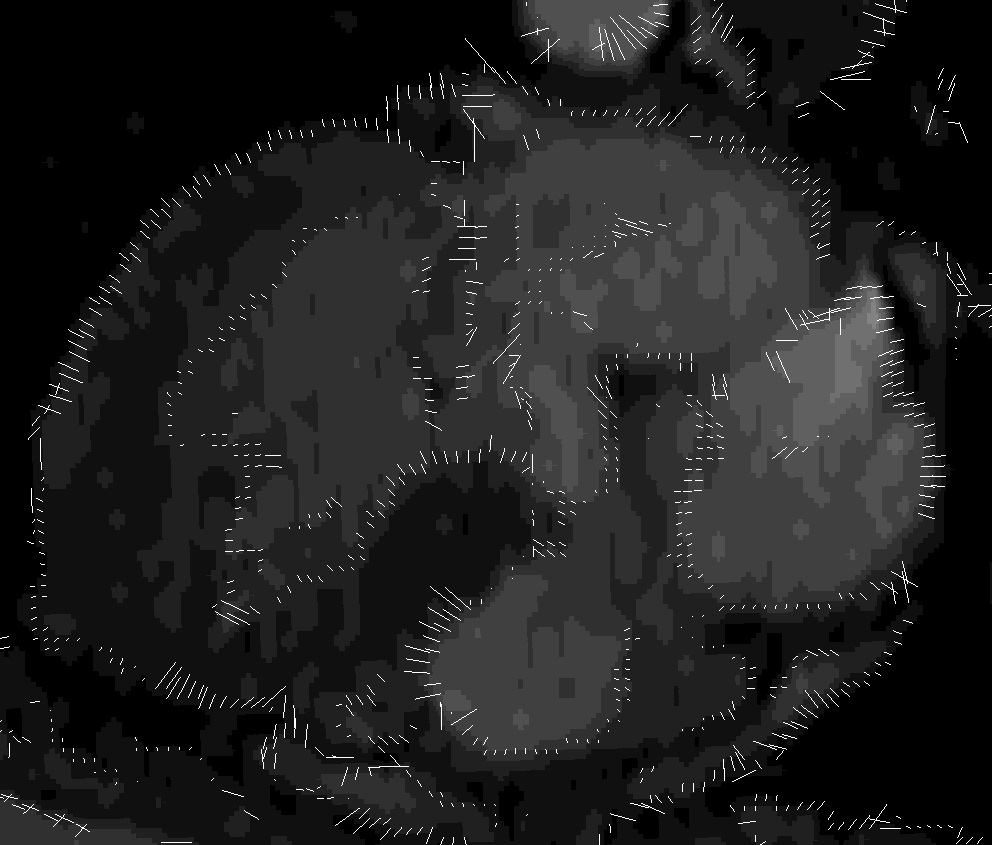
The segmentation is performed iteratively: First, an initial heart contour is semiautomatically created for the MRT dataset of the first time slot, wherefore a 3D physically based deformable model is applied. Using the result of the segmentation of the prior dataset as an initial contour, the segmentation is repeated for all images of the scan sequence. The deformation is influenced by the image forces and the optical flow.

Optical flow in transversal MRT image of heart

Frontal view of heart movement (Animation in Quicktime format 150 kB)

Rotating view of heart movement (Animation in Quicktime format 12 MB)

Interactive Deformation

In the section a way is shown, to deform surface meshes interactively. The deformation of the surface meshes allows

the manual segmentation of medical images
the construction of initial contours.

The deformation is performed applying the radial-basis-function-transformation [Sachse98]. Additionally, the neighbourhood relations in the surface mesh are taken into account.

The deformation process is visualized 2 and 3 dimensional in combination with surface and volume based representations of medical images. This allows the real time control of the image segmentation and of the initial contour construction.

The interactice deformation of surface meshs can be applied in conjunction with the traditional methods of image segmentation, eg

Thresholding
Regiongrowing

Hereby, the surface meshes serve to mask regions in which the traditional methods are applied.

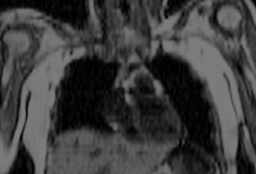
Manual segmentation of the Visible Female heart

Segmentation of the Visible Female heart using interactive deformation of surface meshes (Model in zipped VRML format 4.4 MB)

Segmentation of the Visible Female heart using interactive deformation of surface meshes and traditional techniques (Animation in Quicktime format 1.5 MB)

Topological Adaption

Topologically adaptable deformable models are a significant extension of the traditional deformable models. The extension allows the

melting
splitting

of surface meshes.

Here, an efficient topologically adaptable deformable model is presented. The topological adaption is performed as additional step following an iteration of the explicit Euler-forward-integration. The step consists of

intersection of the surface mesh with an isotropic equidistant lattice
classification of lattice nodes. Determined is, if nodes are inside or outside of the mesh.
reconstruction of the mesh using the Marching-Cube algorithm

Additional to the topological adaption, the application of the method delivers a limitation of the size of the surface mesh element. This property is of advantage for the segmentation of geometric complex objects.

Original mesh and lattice

Publications

2000

L. Thomas, F. B. Sachse, C. D. Werner, and O. Dössel, "Topologisch veränderbare dreidimensionale Aktive Konturen in der medizinischen Bildverarbeitung", to appear in Proc. 34. Jahrestagung DGBMT, 2000
P. Zerfass, C. D. Werner, F. B. Sachse, and O. Dössel, "Deformation of surface nets for interactive segmentation of tomographic data", to appear in Proc. 34. Jahrestagung DGBMT, 2000

1998

N. H. Busch, F. B. Sachse, C. D. Werner, and O. Dössel, "Segmentation klinischer vierdimensionaler magnetresonanztomographischer Aufnahmen mittels Aktiver Kontur Modelle und haptischer Interaktion," Biomedizinische Technik, vol. 43, Supplement 1, pp. 526-529, 1998
C. D. Werner, F. B. Sachse, K. Mühlmann, and O. Dössel, "Modellbasierte Segmentation klinischer MR-Aufnahmen," Bildverarbeitung für die Medizin 1998, Hrsg. T. Lehmann et al., Springer Berlin, ISBN 3-540-63885-7, 1998
F. B. Sachse, "Modelle des menschlichen Körpers zur Berechnung von physikalischen Feldern," Shaker Aachen, ISBN 3-8265-3498-0, 1998