Dipl.-Math. Danila Potyagaylo, Dipl.-Ing. Walther Schulze

Antonia Reinke

Download as PDF

Motivation
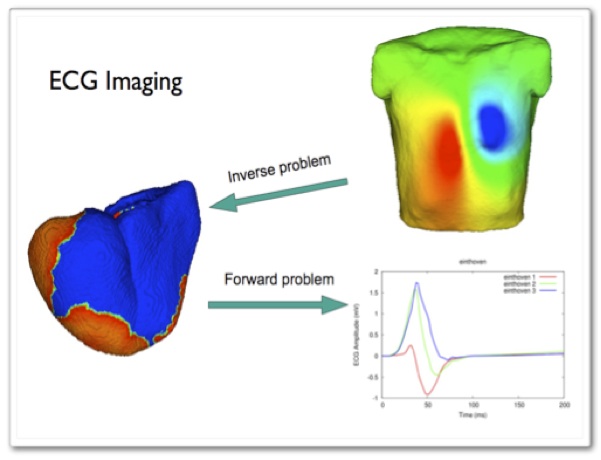
The goal of ECG imaging is the reconstruction of cardiac electrical sources from the BSPM (body surface potential map). The tool could have a great clinical potential by providing a cardiologist quantitative information about the heart condition, thereby enabling pre-interventional planning and facilitating the intervention procedures themselves.

With the knowledge about model geometry, a linear relationship between heart sources and BSPM can be established. The problem is however severely ill-posed, i.e. it is very sensitive to the measurement and modeling errors. Therefore a special mathematical technique, called regularization, should be applied in order to get a stable solution.

Tasks
In this project new approaches for determination of an optimal regularization parameter will be investigated. The measurement errors are unavoidable, therefore we will concentrate on the modeling errors coming mostly from uncertainty about body electrical conductivities. Using explicit integrals formulae for the potentials on the body surface, the dependency of lead fields on conductivities could be derived. This would allow to efficiently use Morozov discrepancy and other principles assuming modeling error estimates are known.

Requirements

• programming skills in C++, MATLAB
• linear algebra, analysis
• some knowledge about optimization and/or cardiac physiology would be a plus